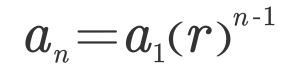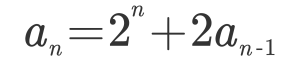Viral video games create math problems
Just a few days before our Calculus I class dove into the final unit on sequences and series, Jacob came to school one morning sharing the hottest new viral video game. 2048 is an unbelievably simple and addictive game where you move numbered tiles around a board. Identical tiles combine to create a new tile whose number is the sum of its parts. 2+2=4. 4+4=8. 8+8=16. You get the idea. Instead of me explaining exactly how it works, click here and play the game for yourself (use the arrow keys). Just do yourself a favor, and set a timer.

The first thing we notice, is that this game supports familiarity with even powers of two. 2, 4, 8, 16, 64, 128,……,2048 is a geometric sequence where the ratio between two consecutive terms is always 2. I knew we would be covering these sequences within the next week and the students tricked me into a promise that we’d study the game (in their minds, play the game) in class. The wheels started turning and I found myself addicted as well while thinking up a project. Ok, now go back and play another round, this time paying attention to the scoring system. Can you identify the pattern?
We see that each time you join two tiles to create a new one, you score points equal to the tile you just created. 2+2 gets you 4 points. 16+16 gets you 32 points. So this observation raises a new question. If you are able to get the 2048 tile, what will your score be? 2048? Not exactly, because you’ve also accumulated points for every tile up to that point. This led me to think we may be looking at a geometric series problem, also a topic in our upcoming unit.
These hints at relevance to our current course of study were enough to let me come up with a few questions and leave the problem solving up to the students.
First an easy question to warm up. What is the value of the n-th tile? In other words, what is the number on each tile as a function of which tile it is the the sequence 2, 4, 8, 16…..? They quickly arrive at the sequence rule:
From this, we can determine what the largest tile you can possibly get on a 16-square board is. Since you’ll need one of each tile in the entire sequence to build it all up, you could have a 2, a 4, an 8, a 16 and so on. When you combine them all, you’d get the 17th tile, which is
Of course, those who play the game a lot might notice that each move you make, you get a new tile. That new tile is randomly either a 2 or a 4, so if you get lucky enough to draw a 4, you could theoretically arrive at the 18th tile, 262144. Please don’t spend the next two weeks trying.
The tougher question I posed was: What is the value of the n-th tile? The second tile (4) is worth 4 points, but the 3rd tile (8) has a total value of 16, because it includes 8 points for making the tile, plus 4 points for each of the tiles that went into it. The 4th tile (16) is worth 48 points by the same logic.
The pattern of numbers we see is 4, 16, 48, 128…… So what is the pattern? Well, it’s not readily apparent, for this is neither an arithmetic or geometric sequence. An arithmetic sequence is defined by a common difference d between each successive term. e.g. 0, 5, 10, 15, 20…… d=5 and the sequence rule is given by
A geometric sequence is defined by a common ratio r between successive terms, such as 3, 9, 27, 81…… and the sequence rule is:
Our problem at hand involved a combination of the two.
The prompt got wheels turning, students arguing with each other and going back and forth between swiping tiles up, down, left, and right on their iPads and scribbling funny greek symbols and subscripts all over their paper. After several hypotheses were concocted, tested, and abandoned, they arrived at a fairly simple way of describing the pattern, which was to use a recursive formula
Which simply states what I discussed earlier and that the value of any tile is simply the number on that tile plus twice the value of the tile that came before it.
This is valid, but somewhat inconvenient in that if we want to find the value of the elusive 18th tile, we’d have to find the value of all 17 tiles before it. We want to cut to the chase. At this point, if you’re still reading, it’s apparent that you have some interest in the mathematics of sequences and series. I’d hate to deprive you of such an interesting puzzle to solve. So play with it a while, and see if you can come up with a rule that works. I’ve already give you several hints and a frustrating new perspective on such a simple game. If you decide to give up, just track down one of our calculus students and they can fill you in!
-Dan Thurber, Math Teacher
And if you ever get this far, there’s really nothing left to prove…